Erstveröffentlichung im März 2010 in der Fairplay 91.
>>Direkt zum Postscriptum springen.
Kreis, Dreieck, Kreuz. Ganz abstrakt und völlig ohne Thema füllen die Spieler ihr Tableau aus. Einer würfelt und gruppiert die vier Würfel in eine ihm genehme, zusammenhängende Formation. Jeder Würfel zeigt mit gleicher Wahrscheinlichkeit eine der drei eingangs genannten Figuren. Alle Spieler müssen diese nun in der vorgegebenen, aber beliebig gedrehten Anordnung auf ihrem sieben mal sieben Felder großen Tableau eintragen. Dabei dürfen bis zu drei Würfel „über den Rand“ hinausragen und somit verfallen.
Wozu das Ganze? Nur Gebiete, die mindestens fünf gleiche, zusammen hängende Symbole enthalten, kommen in die Wertung. Die Rechnung ist ganz einfach: Anzahl der Wertungsgebiete mal Anzahl der in ihnen enthaltenen Felder. Damit ist der Fahrplan klar: Lieber mehrere kleine als ein großes Gebiet bilden!
Mit der Anordnung der Würfel ist reihum jeder mal an der Reihe. Bei zwei Spielern kann man entsprechend doppelt so oft Einfluss nehmen wie zu viert. Dadurch skaliert MOSAIX mit der Spielerzahl. Ansonsten finden kaum Wechselwirkungen zwischen den Spielern statt. Freilich kann man bei der Gruppierung der Würfel auf die Nachbartableaus schauen, um Vorlagen zu vermeiden. Doch meist ist man auf das eigene Vorankommen bedacht.Während einer Partie MOSAIX ist es ruhig am Spieletisch. Zuerst muss der würfelnde Spieler entscheiden, wie er die Würfel platziert. Dabei haben die anderen Pause. Lieber nicht hinschauen und auf eine günstige Formation hoffen – sonst ist die Enttäuschung groß, wenn nochmal umgruppiert wird! Sobald die Würfel zur Eintragung freigegeben sind, lehnt sich der würfelnde Spieler für einen Moment zurück. Doch diese Wartephasen sind kurz genug, um nicht ins Gewicht zu fallen. Jeder ist genügend mit seiner Aufgabe der Optimierung beschäftigt. Zum Ende hin nimmt die Spannung zu. Gelingt es noch, dieses Gebiet auf fünf Symbole zu bringen und damit den Faktor zu verbessern? Sobald ein Spieler keine Würfelergebnisse mehr eintragen kann, endet das Spiel. Die auf dem Tableau eingetragene Wertungstabelle vereinfacht das Zusammenzählen und hat bereits beim Erklären gute Dienste geleistet. Zusammen mit dem günstigen Preis um 6 Euro eine rundum gelungene Sache!
Kathrin Nos
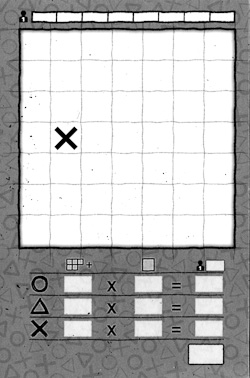
Frage: Wieviele Fünfergruppen einer Sorte lassen sich auf dem Mosaix Tableau unterbringen?
Nun, das Feld ist 7 mal 7 = 49 Felder groß, wenn gleiche Gruppen einander berühren dürften wäre also Platz für 9 Stück. Jede Gruppe hat aber mindestens 4 Grenzfelder, selbst wenn sie in einer Ecke liegt. Jedes Grenzfeld kann maximal von 4 Gruppen genutzt werden, damit reduziert sich die maximale Gruppenzahl auf 8. Diese Zahl ist immer noch zu optimistisch geschätzt. So lassen sich die 4 Grenzen von Eckgruppen an höchstens fünf anderen Feldern nutzen. Damit ist für diese die Mehrfachnutzung maximal (5+1)/4 = 1,5. Dies bedeutet: Schon die Eckgruppen haben eine effektive Größe von 5+4*4/6 > 7,6. Bleiben also höchstens 49-4*7,6 = 18,6 Felder übrig. Damit passen höchstens 7 Gruppen aufs Feld. Die restlichen Gruppen haben aber mindestens so sie am Rand liegen 5 und in der Mitte 9 Grenzfelder. Es ist wohl nicht zu vermuten, dass sich für sie eine kleinere effektive Größe ergibt. Damit reduziert sich die gesuchte Zahl auf vermutlich 49/7,6 < 7. Nun lassen sich Lösungen mit 6 Gruppen einfach konstruieren. Wer will darf dies selbst per Folienschreiber auf den Bildschirm in die Abbildung hineinmalen.

Prädikat:
1 von 3 Mosaiken
Zusatzfrage: Gibt es eine einfache präzisere Abschätzung ohne waghalsige Vermutung im Mittelteil? Oder noch besser: Liege ich falsch und schafft es jemand doch 7 Gruppen einer Sorte ins Quadrat zu quetschen? Über ein Bildschirmfoto der Konstruktion wäre ich hocherfreut.
Peter Nos